大家好，今天我们要聊的是快速排序，一种性能更好的排序算法。那我们开始吧！Let's go ！

快速排序

快速排序比冒泡排序、选择排序、插入排序的性能都要好，也是以一种用于实战的排序算法，Chrome曾经就用它作为sort的排序算法。

快速排序的思路

• 分区：从数组中任意选择一个 ，所有比基准小的元素放在基准前面，比基准大的元素放在基准的后面。

• 递归：递归地对基准前后地子数组进行分区。

快速排序动画

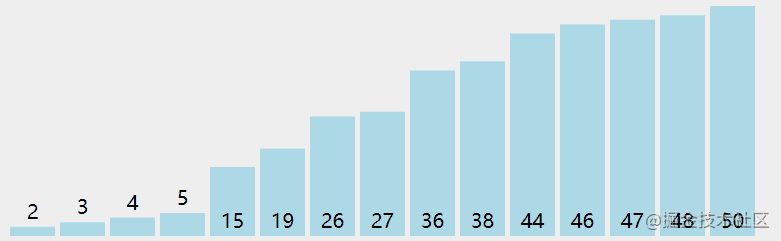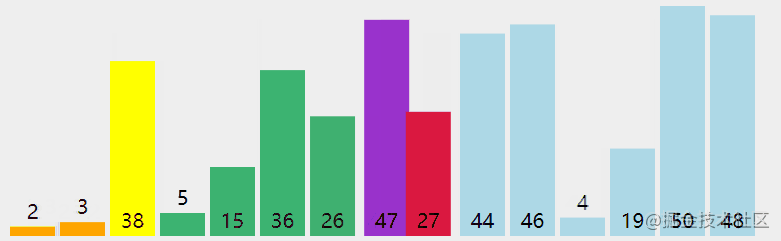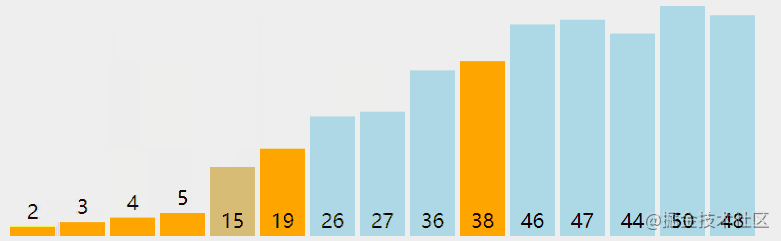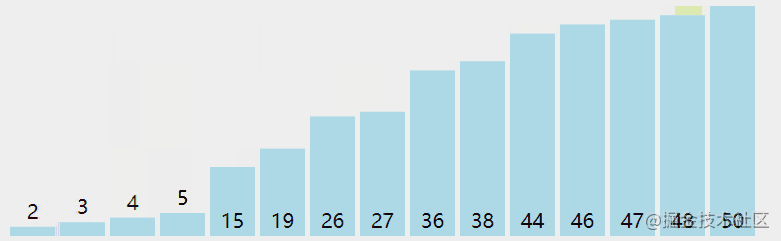
• 首先选择数组中任意一个作为基准，既然是任意，就以数组地第一个作为基准。

• 为当前基准。

• 然后对数组进行挨个比较， 为当前比对地元素。

• 比基准大的为，小的为。

• 一轮循环后，把 基准插入到所有绿色后面。

• 就完成了整个分区操作。

• 接下来对前后两个分区递归进行如上分区操作。

• 就可以完成整个排序了。

实现

Array.prototype.quickSort = function () {
    const rec = arr => {
        if (arr.length === 1) return
        const left = []
        const right = []
        const mid = arr[0]
        for (let i = 1; i < arr.length; i++) {
            if (arr[i] < mid) {
                left.push(arr[i])
            } else {
                right.push(arr[i])
            }
        }
        return [...rec(left), mid, ...rec(right)]
    }
    const res = rec(this)
    res.forEach((n, i) => { this[i] = n })
}
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
arr.quickSort()
console.log(arr);
// [
   2,  3,  4,  5, 15, 19,
  26, 27, 36, 38, 44, 46,
  47, 48, 50
]

快速排序的时间复杂度

• 递归的时间复杂度是 O（logN）。

• 分区操作的时间复杂度是 O（n）。

• 时间复杂度：O（n * logN）。

End~~~