作者：John Schulman（OpenAI）

译者：朱小虎 Xiaohu (Neil) Zhu（CSAGI / University AI）

原文链接：http://joschu.net/blog/kl-approx.html

术语： 散度（ Divergence）; 近似（Approximation）; Monte-Carlo 估计（Monte-Carlo estimator）

本文讨论 散度的 Monte-Carlo 近似：

这解释了之前使用了一个技巧，针对来自 中的样本 以 样本平均来近似 ，而不是更加标准的 . 本文谈谈为何该表达是一个 散度的好的估计（尽管有偏 biased），以及如何让其变得无偏（unbiased）保证其低方差。

我们计算 的选择取决于对 和 的访问方式。这里，我们假设能够对任意 计算概率（或者概率密度） 和 ，但是我们不能解析地跑遍 求和。为何我们不能解析地计算呢？

最常用的估计求和或者积分的策略是使用 Monte-Carlo 估计。给定样本 ，我们如何构造好的估计？

一个好的估计是无偏的（即有正确的均值）并且低方差。我们知道一个无偏估计（在从 中采样的样本下）是 。但是，它有高方差，因为它对样本的一半是负，而 散度总是为正。让我们称此简易估计 ，其中我们已经定义了比例 后面也会多次出现此值。

另一个替代估计有低的方差不过是有偏的，即 。我们不妨称此为 。直觉上看， 看起来更加好因为每个样本告诉了我们 和 之间相距多远，并且总为正。实验上看， 实际有比 更低的方差，并也有相当低的偏差（bias）（下面在实验中给出此点）。

关于估计 为何有低偏差有一个很好的原因：其期望是一个 [-散度（divergence）](https://en.wikipedia.org/wiki/F-divergence)。一个 -散度 被定义为关于一个凸函数 ，。 散度和其他有名的概率距离均是-散度。现在这是关键的难以被发现的事实：所有具有可微函数 的 -散度与 散度当 接近 时的二阶。也就是说，对一个参数化分布 ，

其中 是关于 的 Fisher 信息矩阵在 的值。

期望 是 -散度，其中 ，而 对应于 。易见，两者均有 ，所以两者看起来对 有相同的二阶距离函数。

是否可以写出一个 散度估计既是无偏又是低方差的呢？一般达成低方差的方法是通过一个控制变量。就是说，取 并加上某个期望为零但是与 负相关的量。保证期望为零唯一有趣的量是 。所以，对任意的 ，表达式 是 的无偏估计。我们可以做一些计算来最小化这个估计的方差，对 求解。但不幸的是，我们获得一个表达式，它依赖于 和 并难以解析地计算。

但是，我们可以使用一个更为简单的策略来选择一个好的 。注意因为 是凹函数，。因此，如果我们令 ，上面的表达式会确保为正。它度量了 和它的切线的竖直距离。这让我们有了估计 。

通过看凸函数和它切平面的差距来度量距离的想法出现在很多领域。这杯称为 [Bregman 散度](https://en.wikipedia.org/wiki/Bregman_divergence)并有很多优美性质。

我们可以推广上面想法来获得一个好的，总是为正的对任何 -散度的估计，大多数明显是另一个 散度即 （注意这里的 和 调换了次序）。因为是凸函数，并且，下面是 -散度的一个估计：。这总是为正因为它是和其在 处的距离，并且凸函数在它们的切线上方。现在 对应于 ，其有 ，使得我们有了估计 。

总结一下，我们有下列估计（对样本 和 ）：

现在我们比对这三个对 估计的偏差和方差。假设。这里正确的散度为 。

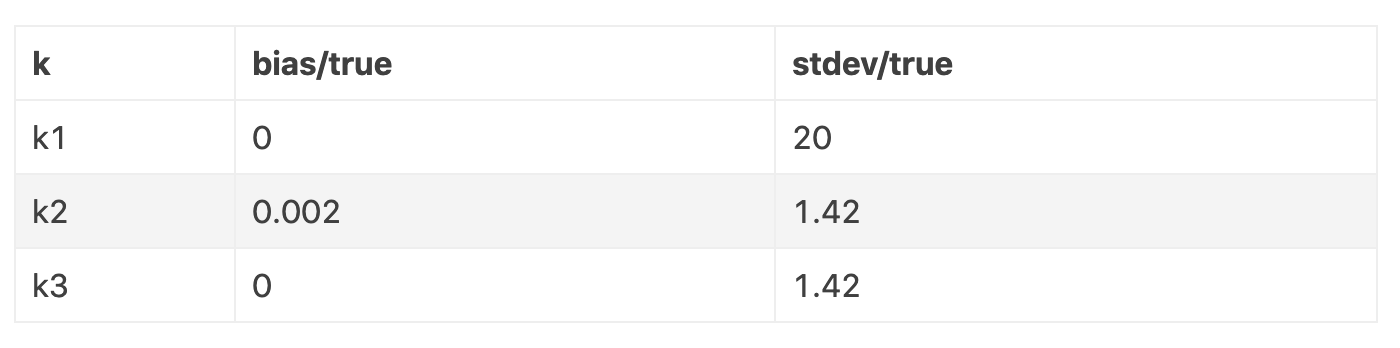
注意 的偏差非常低：为 0.2%。

现在我们尝试对大一些的 散度近似。 给我们一个真实 散度为。

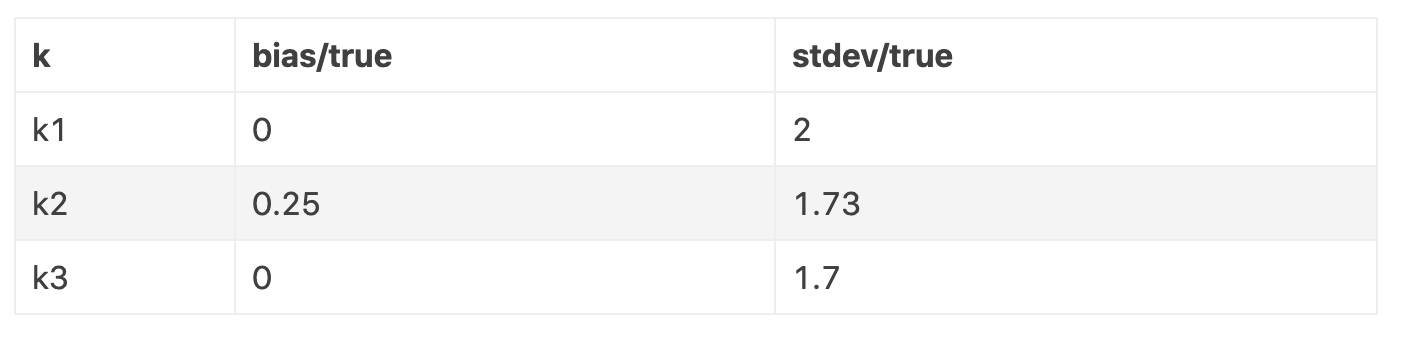
这里， 的偏差更大一些。 甚至有比 更低的标准差同时还是无偏的，所以它看起来也是在一个严格意义上更好的估计。

这里是我用来产生这些结果的代码：

import torch.distributions as dis
p = dis.Normal(loc=0, scale=1)
q = dis.Normal(loc=0.1, scale=1)
x = q.sample(sampleshape=(10000000,))
truekl = dis.kldivergence(p, q)
print("true", truekl)
logr = p.logprob(x) - q.logprob(x)
k1 = -logr
k2 = logr ** 2 / 2
k3 = (logr.exp() - 1) - logr
for k in (k1, k2, k3):
    print((k.mean() - truekl) / truekl, k.std() / truekl)