实测 Google 全同态加密FHE,效果如何?
Google 开源了首个通用全同态加密(FHE)的转译器(transpiler),可以将普通的 C++程序转译为基于 TFHE 同态库的同态程序,将明文运算转换为了同态密文运算。
作为多方安全学习领域的大事件,我和小伙伴当然高度关注,于是对 FHE 做了一下测试,并且在其基础上运行了 Avatar阿凡达2.0 纵向逻辑回归组件。话不多说,先上结论:
好处:FHE的转译模式可以大量减少使用同态加密编程成本的工作量。在不存在转译库的情况下,一行简单代码需要修改成十几行加密位运算代码才可以完成加密运算。
短板:但从测试结果上看,我们认为 FHE 目前还是为概念验证性项目,无法完整支持基础运算算子(浮点数,除法),运行时间太太太太长,且文档仍不完整,不适合用于产品开发。
系统性能
Intel Core i5-10400 CPU @ 2.90GHz x 12
运行中我们使用6核
不能做的事情
根据Google同步发布的白皮书,以下编程逻辑现阶段无法实现:
XLS 库在转译过程中无法获得外部数据信息,所以由外部数据决定的控制流语句(分支,循环)无法转译;
XLS 库只能转译固定数量的循环和固定长度的数组;
指针操作,递归函数无法转译;
因为 FHE 库局限性,浮点数,长整型数,浮点的除法计算不支持;
运行时间
我们首先运行了google提供的示例文件(在官方git库中/transpiler/examples中)。
简单两位数算术运行:
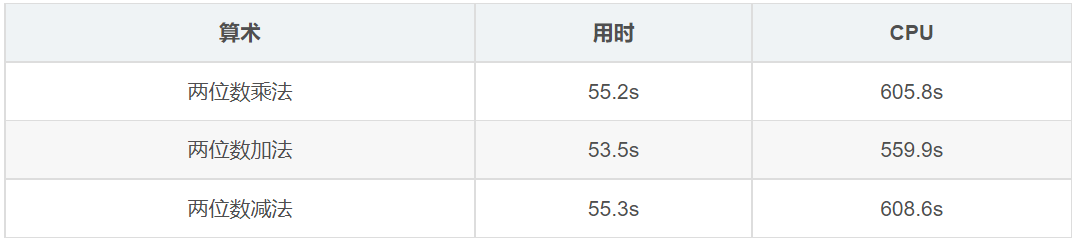
ibonacci:
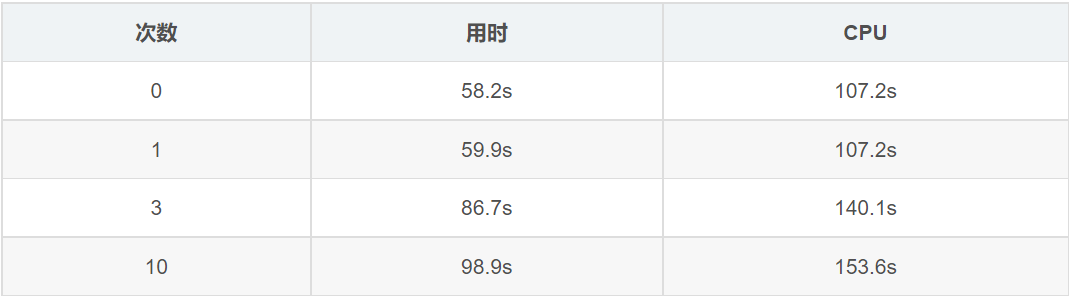
在谷歌提供的示例程序之外,我们还针对我们联邦学习的需求开发了向量运算的示例程序:
#include "calculator.h"
#pragma hls_top
void CalculateByVector(int my_list[10]) {
#pragma hls_unroll yes
for (int i = 0; i < 10; ++i) {
my_list[i] = my_list[i] * my_list[(i + 1)%10];
}
}输入数组 x:{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

优化性能测试
XLS 在将高级语言转译成为底层逻辑后,还会对其进行优化,我们在向量运算中测试了可优化的语句:
x(i) = x(i) + x(i)
x(i) = x(i) * 2
x(i) = x(i) * 8上述语句对一个数组进行运行速度为 0.0005s,比较之前有了大数量级的提升。
然而,如果我们的乘法不能转化为二进制移位运算,或者在上述语句中追加一些简单的逻辑重新编译后:
x(i) = x(i) + x(i) + 2
x(i) = x(i) * 3运行速度又变成了770s和 517s,可见优化的条件非常苛刻。
于是我们认为
FHE 库现阶段只是验证性项目,概念新颖,全同态加密转译器在多方安全计算应用方面有算法方面和开发便利度的优势,但现阶段计算运行时间过长,我们本计划在其基础上运行 Avatar阿凡达2.0 纵向逻辑回归组件,结果一个简单数据矩阵数乘(3x3矩阵)就要花费无法接受时间(900s)。
再就是功能方面,无法完整支持基础运算(浮点数,除法),可用性不强,全同态距离真正实用还有一段距离。