众所周知，电流（C/s）=磁场强度（C/m^3）*面积（m*3）*速度（m/s）

如果我们用单位对该公式进行“代数运算”，会得到

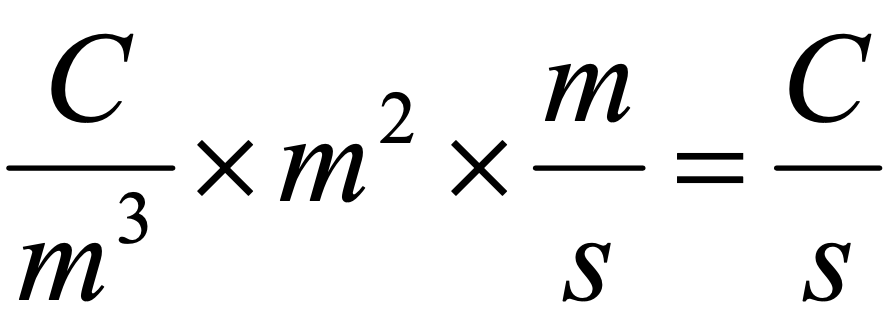
现在，这看起来似乎很浅显，但是它为我们提供了一个有用的方法，用于检查我们的公式是否正确。如果在计算时发现将3C电荷乘以6m距离可获得9N的结果；或者将13m/s的速度乘以40s的时间得到520A的电流，您都一定犯错了！

我们还可以使用单位必须平衡的原理来猜测我们不知道如何推导的方程式。例如，通过猜测一个简单的摆锤的运动周期可能取决于摆锤L的长度，局部重力g的强度和摆锤的质量m。i.e.

• L以米为单位

• g以N / kg或m / s2为单位

• m以kg为单位，

• 并且我们想要得到一个周期，以s为单位。

可以将这些测量值组合成s的唯一方法是取L，将其除以g，然后取平方根。因此，在不了解简单谐波振荡器的任何物理原理的情况下，我们证明了摆与L/g开根号有关，并且独立于质量m。

同样，请注意如果将欧姆乘以法拉第会发生什么：

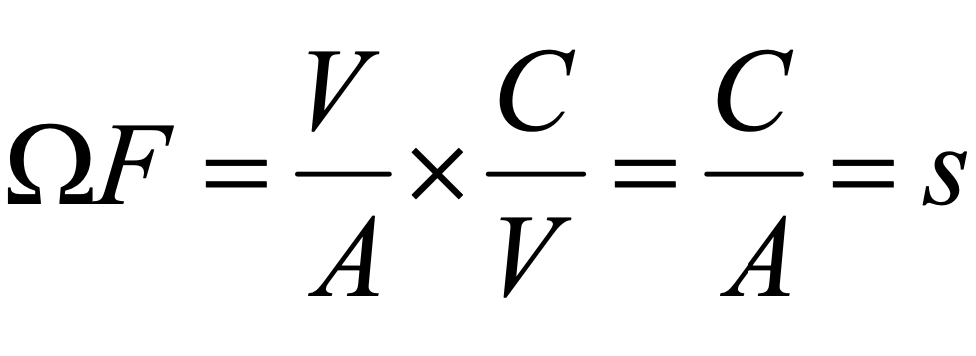
是的，您得到秒。因此，如果将电容器（电阻网络）的电阻加倍，则充电或放电所需的时间将是原来的两倍，这不足为奇。

当然，如果公式中存在具体系数，仅通过量纲分析就无法得知了。