写在前面：

大家好，我是时光。

今天给大家带来的是排序算法中的堆排序，这种排序跟二叉树相关。我采用图解方式讲解，争取写透彻。话不多说，开始！

思维导图：

堆排序导图

1，堆排序概念

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

相关概念：

1.1，二叉树

二叉树

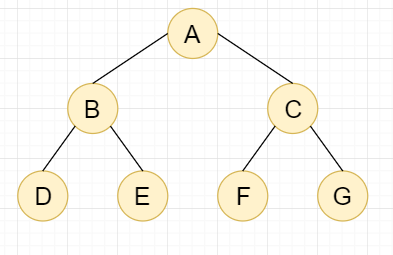
特征：每个节点最多只有2个子节点（不存在度大于2的节点）

1.2，满二叉树

满二叉树

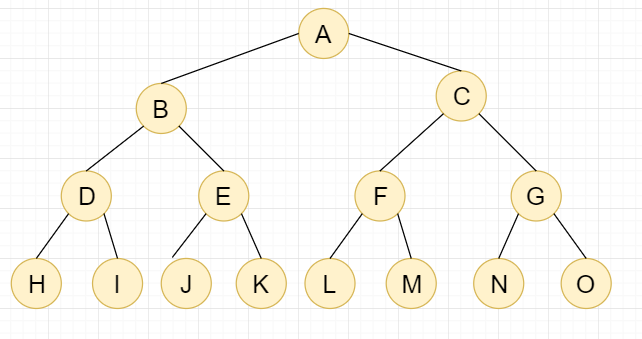
满二叉树：叶子节点全部都在最底层；除叶子节点外，每个节点都有左右孩子；

1.3，完全二叉树

完全二叉树

完全二叉树：叶子节点全部都在最底的两层；最后一层只缺少右边的叶子节点，左边一定有叶子节点；除了最后一层，其他层的节点个数均达到最大值；

1.4，最大堆和最小堆

最大堆：堆顶是整个堆中最大元素

最小堆：堆顶是整个堆中最小元素

2，算法思路

我们先搞清楚这个堆排序思想，先把逻辑搞清楚，不着急写代码。

我们首先有一个无序数组，比方说

int[] arr={4,2,8,0,5,7,1,3,9};

既然用到堆，肯定先要将数组构建成二叉堆。需要对数组从小到大排序，则构建成最大堆；需要对数组从小到大排序，则构建成最小堆。

2.1，第一个步骤，初始化堆

我们先来看看数组是如何存储二叉树的

注意：这里考虑的当前节点，必须是完全二叉树的非叶子节点。并且节点的左孩子和右孩子必须小于数组长度，所以后面需要添加限制条件。

看到上图中的公式，我们明白了数组是可以存储完全二叉树，同时保留节点之间的关系。以上述数组为例

数组存储完全二叉树

那么存储好之后，如何将二叉树构建成二叉堆呢？继续往下看

完全二叉树

以这个图为例，我们以最大堆举例，若要构建二叉堆，则A要比B和C都大，B要比D和E都大，C要比F和G都大。也就是说父节点要比子节点都大才行。

记录数组下标的二叉树

在这个图中，明显不满足最大堆的要求。我们先拿序号为3,7,8的三个节点来研究，i=3的节点比i=7和i=8的节点都小，所以需要交换位置。注意此图是从0开始，也就是模拟数组下标从0开始。

怎么交换呢？很简单。我们看节点0，设为当前节点，那么它的，它的；注意下标从0开始。

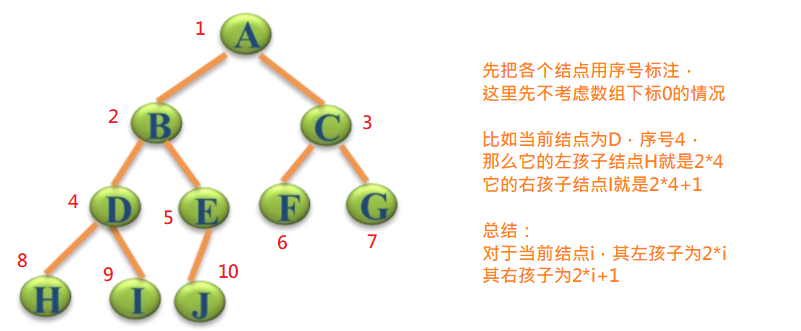
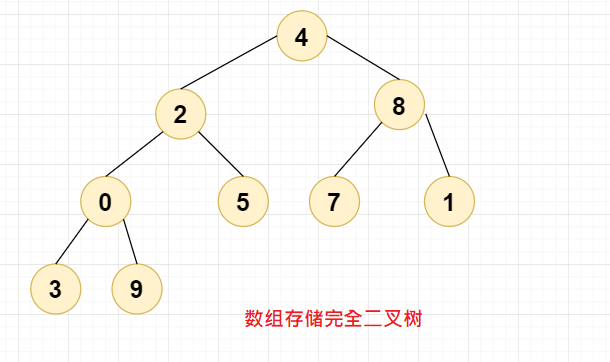
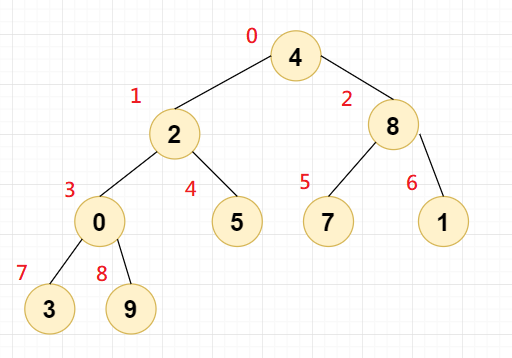
//初始化堆
public static void HeapAdjust(int[] arr,int index,int len){
        //先保存当前节点的下标
        int max = index;
        //保存左右孩子数组下标
        int lchild = index*2+1;
        int rchild = index*2+2;
        //开始调整，左右孩子下标必须小于len，也就是确保数组不会越界
        if(lchild arr[max]){
            max=lchild;
        }
        if(rchild arr[max]){
            max=rchild;
        }
        //若发生了交换，则max肯定不等于index了。此时max节点值需要与index节点值交换，上面交换索引值，这里交换节点值
        if(max!=index){
            int temp=arr[index];
            arr[index]=arr[max];
            arr[max]=temp;
            //交换完之后需要再次对max进行调整，因为此时max有可能不满足最大堆
            HeapAdjust(arr,max,len);
        }
    }

上面代码很好理解，中间的两个if语句就是交换节点索引值，只要有一个孩子节点大于，就需要进行交换。若父节点比两个孩子节点都大，那么就不需要交换了。

最后面的if语句是交换节点值，我们知道，只要与和有交换，则一定不等于了！

那为什么最后的语句里面还要加上一个递归写法呢？我们举个例子就明白了，还是以上述数组为例，先看看一轮交换之后的样子：

第一次交换，0与9交换，此时Index=9；

0与9交换

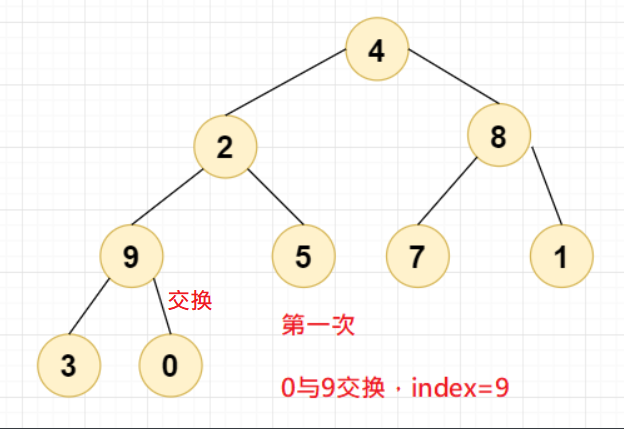
第二次交换，8已经比7和1都大了，此时不需要交换；

第三次交换，2与9交换，此时=9；

2与9交换

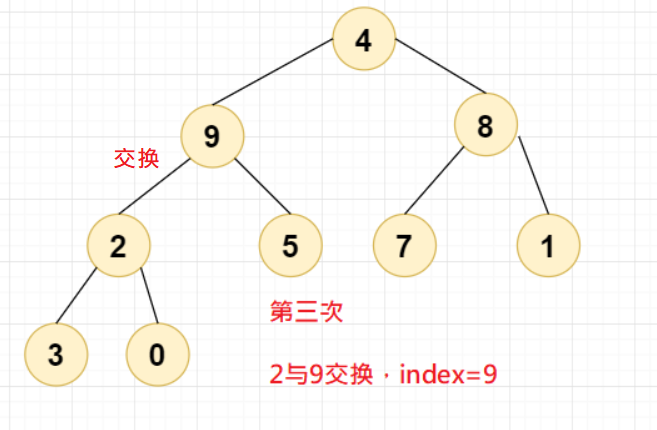
第四次交换，4与9交换，此时=9，第一轮交换到此结束。

4与9交换

一轮结束后，有小伙伴儿已经发现问题了，虽然9成功的成为最大堆的堆顶元素，但是下面的其他元素并不满足最大堆的要求，比如说左下角的元素2,元素3,元素0等这种二叉树就不满足，元素4，元素2，元素5也不满足。

因此在交换节点值这个步骤里，我们需要进行递归操作，交换完之后再次对进行堆调整：

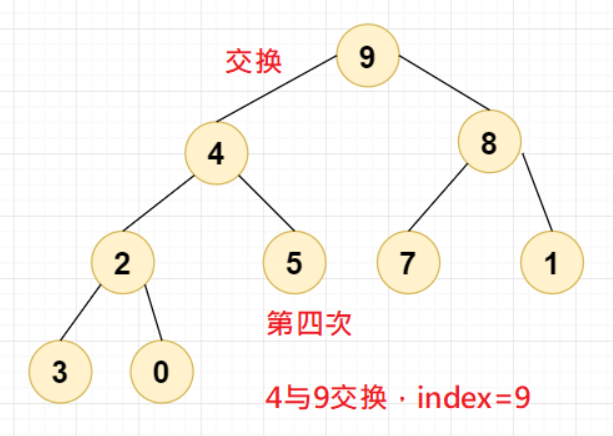
//若发生了交换，则max肯定不等于index了。此时max节点值需要与index节点值交换，上面交换索引值，这里交换节点值
if(max!=index){
    int temp=arr[index];
    arr[index]=arr[max];
    arr[max]=temp;
    //交换完之后需要再次对max进行调整，因为此时max有可能不满足最大堆
    HeapAdjust(arr,max,len);
}

堆排序的测试：

//堆排序
    public static int[] HeapSort(int[] arr){
        int len=arr.length;
        /**
         * 第一步，初始化堆，最大堆，从小到大
         * i从完全二叉树的第一个非叶子节点开始，也就是len/2-1开始(数组下标从0开始)
         */
        for(int i=len/2-1;i>=0;i--){
            HeapAdjust(arr,i,len);
        }
        //打印堆顶元素，应该为最大元素9
        System.out.println(arr[0]);
        return arr;
    }

上述代码就是从完全二叉树的第一个非叶子节点开始调换，还顺便打印堆顶元素，此时应为9；

至此，第一个步骤，初始化堆完成，最后的结果应该为下图：

初始化堆结束

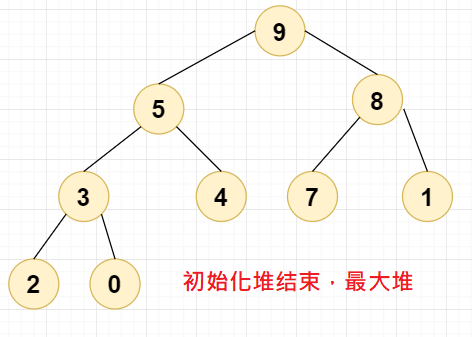
2.2，第二个步骤，堆排序

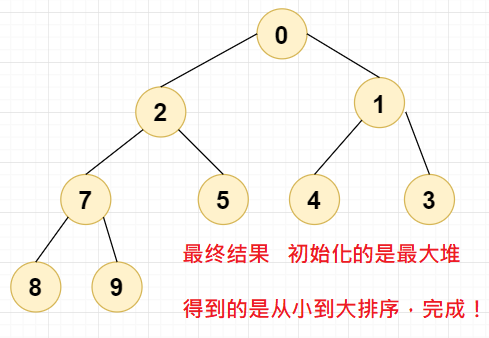
堆排序的过程就是将堆顶元素（最大值或者最小值）与二叉堆的最末尾叶子节点进行调换，不停的调换，直到二叉堆的顺序变成从小到大或者从大到小，也就实现了我们的目的。

我们这里以最大堆的堆顶元素（最大元素）为例，最后调换的结果就是从小到大排序的结果。

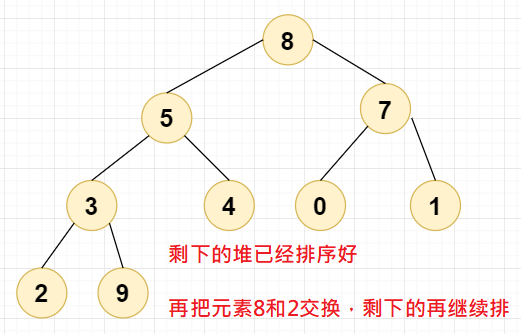
第一次交换，我们直接将元素9与元素0交换，此时堆顶元素为0，设当前节点=0；

0与9交换

这时，我们需要将剩下的元素（排除元素9）进行堆排序，直到下面这个结果：

除元素9以外剩下的元素排序

代码：

/**
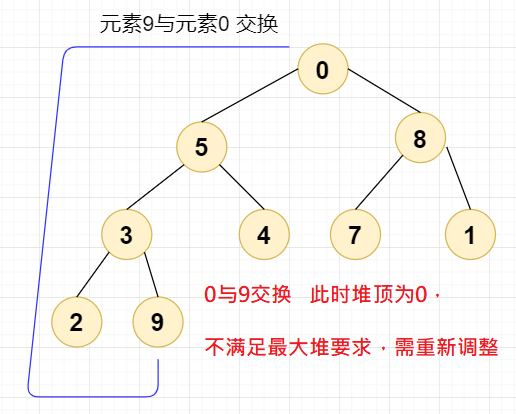
 * 第二步，交换堆顶（最大）元素和二叉堆的最后一个叶子节点元素。目的是交换元素
 * i从二叉堆的最后一个叶子节点元素开始，也就是len-1开始(数组下标从0开始)
 */
for(int i=len-1;i>=0;i--){
    int temp=arr[i];
    arr[i]=arr[0];
    arr[0]=temp;
    //交换完之后需要重新调整二叉堆，从头开始调整，此时Index=0
    HeapAdjust(arr,0,i);
}

注意：这里有个小细节问题，前面我们写的初始化堆方法有三个参数，分别是数组，当前节点以及数组长度，如下：

HeapAdjust(int[] arr,int index,int len)

那么，为何不直接传入两个参数即可，数组长度直接用表示不就行了吗？初始化堆的时候是可以，但是后面在交换堆顶元素和末尾的叶子节点时，在对剩下的元素进行排序时，此时的数组长度可不是了，应该是变化的参数，因为交换之后的元素（比如9）就不计入堆中排序了，所以需要3个参数。

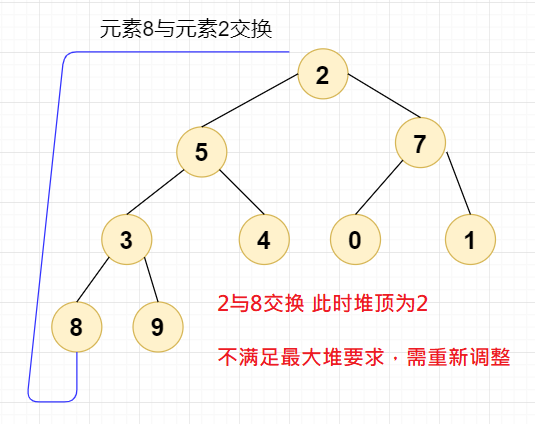
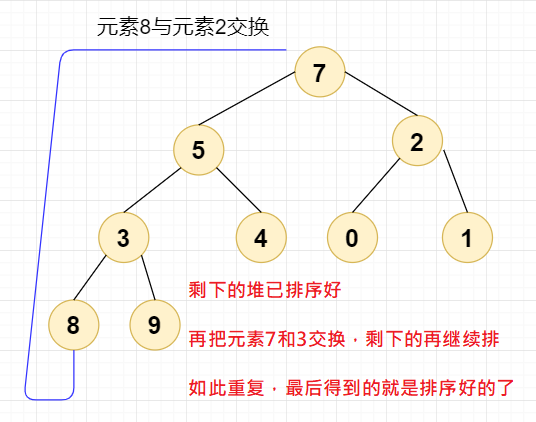
我们进行第二次交换，我们直接将元素8与元素2交换，此时堆顶元素为2，设当前节点=2；

8与2交换

这时，我们需要将剩下的元素（排除元素9和8）进行堆排序，直到下面这个结果：

除元素9和8以外剩下的元素排序

到这个时候，我们再重复上述步骤，不断调换堆顶和最末尾的节点元素即可，再不断地对剩下的元素进行排序，最后就能得到从小到大排序好的堆了，如下图所示，这就是我们想要的结果：

最终排序结果：从小到大

3，完整代码

import java.util.Arrays;

public class Head_Sort {
    public static void main(String[] args) {
        int[] arr={4,2,8,0,5,7,1,3,9};
        System.out.println("排序前:"+Arrays.toString(arr));
        System.out.println("排序后:"+Arrays.toString(HeapSort(arr)));
    }

    //堆排序
    public static int[] HeapSort(int[] arr){
        int len=arr.length;
        /**
         * 第一步，初始化堆，最大堆，从小到大。目的是对元素排序
         * i从完全二叉树的第一个非叶子节点开始，也就是len/2-1开始(数组下标从0开始)
         */
        for(int i=len/2-1;i>=0;i--){
            HeapAdjust(arr,i,len);
        }
        /**
         * 第二步，交换堆顶（最大）元素和二叉堆的最后一个叶子节点元素。目的是交换元素
         * i从二叉堆的最后一个叶子节点元素开始，也就是len-1开始(数组下标从0开始)
         */
        for(int i=len-1;i>=0;i--){
            int temp=arr[i];
            arr[i]=arr[0];
            arr[0]=temp;
            //交换完之后需要重新调整二叉堆，从头开始调整，此时Index=0
            HeapAdjust(arr,0,i);
        }
        return arr;
    }

    /**
     *初始化堆
     * @param arr 待调整的二叉树(数组)
     * @param index 待调整的节点下标，二叉树的第一个非叶子节点
     * @param len 待调整的数组长度
     */
    public static void HeapAdjust(int[] arr,int index,int len){
        //先保存当前节点的下标
        int max = index;
        //保存左右孩子数组下标
        int lchild = index*2+1;
        int rchild = index*2+2;
        //开始调整，左右孩子下标必须小于len，也就是确保index必须是非叶子节点
        if(lchild arr[max]){
            max=lchild;
        }
        if(rchild arr[max]){
            max=rchild;
        }
        //若发生了交换，则max肯定不等于index了。此时max节点值需要与index节点值交换，上面交换索引值，这里交换节点值
        if(max!=index){
            int temp=arr[index];
            arr[index]=arr[max];
            arr[max]=temp;
            //交换完之后需要再次对max进行调整，因为此时max有可能不满足最大堆
            HeapAdjust(arr,max,len);
        }
    }
}

运行结果：

运行结果

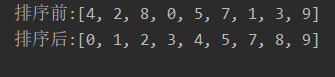
4，算法分析

4.1，时间复杂度

建堆的时候初始化堆过程是堆排序的关键，时间复杂度为，下面看堆排序的两个过程；

第一步，初始化堆，这一步时间复杂度是；

第二步，交换堆顶元素过程，需要用到n-1次循环，且每一次都要用到，所以时间复杂度为；

最终时间复杂度：，后者复杂度高于前者，所以堆排序的时间复杂度为O(nlog n)；

4.2，空间复杂度

空间复杂度是，因为没有用到额外开辟的集合空间。

4.3，算法稳定性

堆排序是不稳定的，比方说二叉树[6a，8，13，6b]，（这里的6a和6b数值上都是6，只不过为了区别6所以这样）经过堆初始化后以及排序过后就变成[6b，6a，8，13]；可见堆排序是不稳定的。

微信搜索公众号《程序员的时光》

好了，今天就先分享到这里了，下期继续给大家带来 排序算法面试内容！

更多干货、优质文章，欢迎关注我的原创技术公众号~