系列文章：

一 摘要

一道典型的动态规划题目，虽然之前在中介绍过了动态规划的原理、应用场景和题目示例，不过也并不是所有人都能熟练掌握（比如我自己...）。

二 题目描述

引用的描述原文如下：

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

限制条件：

三 题目解析

3.1 示例

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

对照题目，12由3个平方数：4 加和得到，所以完全平方数的最少数量是3，故输出为3.

3.2 动态规划解法

既然是典型的动态规划问题，就先考虑动态规划解决。最重要的也就是定义状态转移方程了。f[i] 表示最少需要多少个数的平方来表示整数 i。f[i]的取值一定会是在 [1, √n​]之间，这是有限的整数，也就是可以枚举的。

状态转移方程：

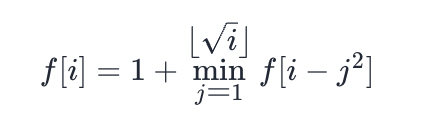
边界条件，也就是当i=0时，f[0]=0 ，实际上我们无法表示数字 0，只是为了保证状态转移过程中遇到 j恰为√i 的情况合法。

Java版代码如下：

public int numSquares(int n) {
        int[] f = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            int minn = Integer.MAX_VALUE;
            for (int j = 1; j * j <= i; j++) {
                minn = Math.min(minn, f[i - j * j]);
            }
            f[i] = minn + 1;
        }
        return f[n];
    }