这是我参与11月更文挑战的第12天。

一、写在前面

LeetCode 第一题两数之和传输门：

LeetCode 第二题两数之和传输门：

今天给大家分享的是LeetCode 数组与字符串 第三题：最长回文子串，为面试而生，期待你的加入。

二、今日题目

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。

示例:

示例 1：

输入: "babad"
输出: "bab"
注意: "aba"也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

三、 分析

这个题目呢，之前参加校IT精英赛时遇到过，当时用c写的，呃···可惜，没写出来，所以咋看第一眼，有点心凉的感觉，当然今日之我已非彼时，早已深知回文字符是个啥玩意，比如日期：2018102，就是个回文字符串。

我是这样想的，要找字符串中最长的回文字符串，肯定就要先找出这个字符串的子串中那些是回文串，然后再求他们中最长的，就可以找到答案了，理清思路，我就开始兴奋的敲代码了，然而...

四、解题

• 方法一：根据上面的思路，一步步来，时间复杂度，嗯，好像有O(n^4)...

class Solution:
  def longestPalindrome(self, s):
    """
    :type s: str
    :rtype: str
    """
    len_s = len(s)
    if len_s == 1:
      return s
    substring = ' '
    substring_set = []
    for i in range(len_s):
      for j in range(len_s):
        if i < j :
          substring = s[i:j+1]
          if self.is_Palindrome(substring) == 1:
            substring_set.append(substring)
    longest_s = ' '
    if substring_set:
      longest_s = substring_set[0]
    else:
      return s[0]
    for i in range(len(substring_set) - 1):
      if len(longest_s) < len(substring_set[i + 1]):
        longest_s = substring_set[i + 1]
    return longest_s
  # 判断是否为回文字符
  def is_Palindrome(self,str_t):
    len_t = len(str_t)
    for i in range(len_t):
      if not str_t[i] == str_t[len_t - 1 - i]:
        return 0
    return 1
s = 'assas'
s0 = Solution()
l_Palindrome = s0.longestPalindrome(s)
print(l_Palindrome)

• 提交结果：

提交之后，老半天，给出结果，运行超时(hhh,结果是对的，就是时间上还有待优化)

• 方法二：对于方法一，无话可说，思前想后，没个结果，百度，嗯，百度是个好东西。从从中心向外扩散，时间复杂度：O(n^2)

'''
思想参考：https://blog.csdn.net/qq_32354501/article/details/80084325
原作者用java实现
'''
class Solution:
  # 类变量，类全局可调用
  longest_s = ''  # 最长回文字符串
  maxLen = 0  # 长度
  
  def longestPalindrome(self, s):
    """
    :type s: str
    :rtype: str
    """
    len_s = len(s)
    if len_s == 1:  # 单字符串
      return s
    for i in range(len_s):
      # 单核(奇数向两边延伸)
      self.find_longest_Palindrome(s, i, i)
      # 双核（偶数向两边延伸）
      self.find_longest_Palindrome(s, i, i + 1)
    return self.longest_s
  
  # 找出最长的回文字符串
  def find_longest_Palindrome(self, s, low, high):
    # 从中间向两端延伸，判断是否为回文字符串的同时寻找最长长度
    while low >= 0 and high < len(s):
      if s[low] == s[high]:
        low -= 1  # 向左延伸
        high += 1  # 向右延伸
      else:
        break
    # high - low - 1 表示当前回文字符串长度
    if high - low - 1 > self.maxLen:
      self.maxLen = high - low - 1
      self.longest_s = s[low + 1:high]

• 提交结果

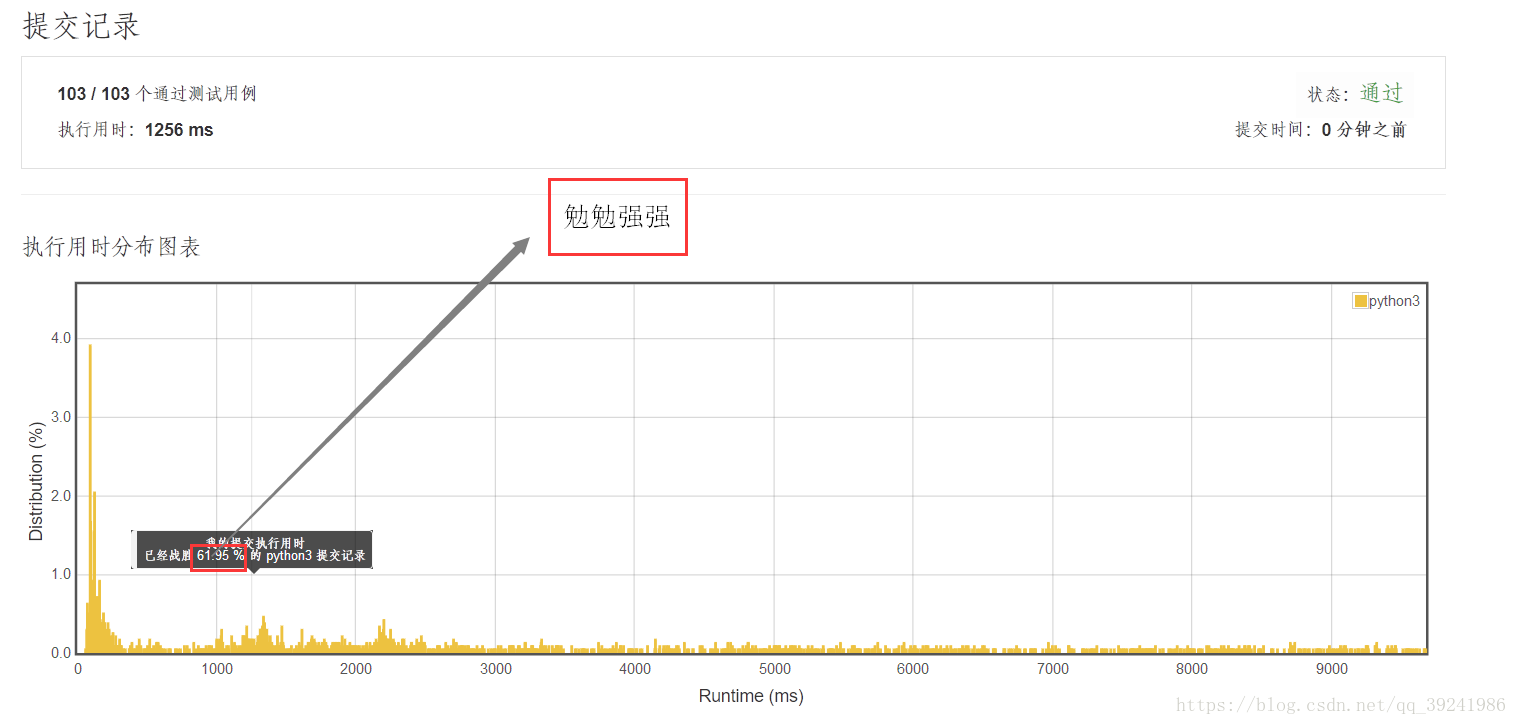
测试数据：103组

运行时间：1256ms

击败人百分比:61.95%

• 方法三：Manacher算法

• 时间复杂度：O(n)

• 算法只有遇到还没匹配的位置时才进行匹配，已经匹配过的位置不再进行匹配，因此大大的减少了重复匹配的步骤，对于S_new中的每个字符只进行一次匹配。所以该算法的时间复杂度为O(2n+1)—>O(n)（n为原字符串的长度），所以其时间复杂度依旧是线性的。

class Solution:
  def longestPalindrome(self, s):
    """
    :type s: str
    :rtype: str
    """
    t0 = '#'.join(s)
    s_new = '#' + t0 + '#'
    len_new = []
    sub = '' # 最长回文字符串
    sub_midd = 0  # 表示在i之前所得到的Len数组中的最大值所在位置
    sub_side = 0  # 表示以sub_midd为中心的最长回文子串的最右端在S_new中的位置
    for i in range(len(s_new)):
      if i < sub_side :
        # i < sub_side时，在Len[j]和sub_side - i中取最小值，省去了j的判断
        j = 2 * sub_midd - i
        if j >= 2 * sub_midd - sub_side and  len_new[j] <= sub_side - i:
          len_new.append(len_new[j])
        else:
          len_new.append(sub_side - i + 1)
      else:
        # i >= sub_side时，从头开始匹配
        len_new.append(1)
      while ((i - len_new[i] >= 0 and i + len_new[i] < len(s_new)) and (s_new[i - len_new[i]] == s_new[i + len_new[i]])):
        # s_new[i]两端开始扩展匹配，直到匹配失败时停止
        len_new[i] = len_new[i] + 1
        
      if len_new[i] >= len_new[sub_midd]:
        sub_side = len_new[i] + i - 1
        sub_midd = i
    a0 = int((2 * sub_midd - sub_side)/2)
    b0 = int(sub_side / 2)
    sub = s[a0 :b0 ] # 在s中找到最长回文子串的位置
    return sub

• 提交结果

• 

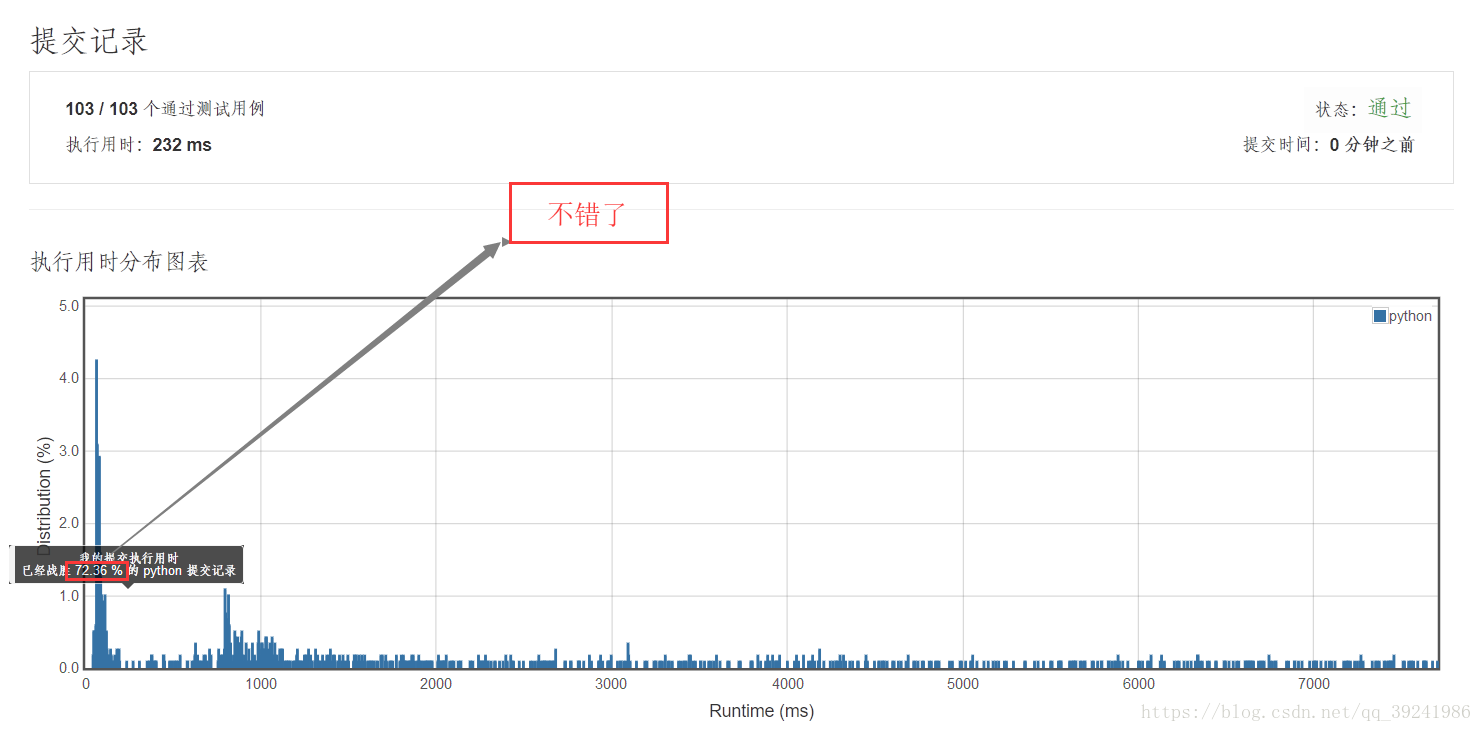
测试数据：103组

运行时间：232ms

击败人百分比:72.36%

五、结语

坚持 and 努力 ： 终有所获。

思想很复杂，

实现很有趣，

只要不放弃，

终有成名日。

—《老表打油诗》

下期见，我是爱猫爱技术的老表，如果觉得本文对你学习有所帮助，欢迎点赞、评论、关注我！