计算机视觉算法探究:OpenCV CLAHE算法详解| 社区征文
一、引言
2021年10月开始学习OpenCV对比度受限的自适应直方图均衡CLAHE,应用编程简单,了解详细算法却相当难。
创建CLAHE对象时,只传递了两个参数:clipLimit和tileGridSize,其中clipLimit是裁剪限制参数,tileGridSize图像的分块个数。关于参数含义及相关的介绍请参考《》。
CLAHE算法的基本步骤如下:
看起来并不难,但在学习时查阅了各种公开资料,发现并不能解答学习时思考的一些问题,如:
经过近4个多月断断续续性的学习,特别是对OpenCV自适应直方图均衡CLAHE源代码的深入解读,这些问题都得到了解决,下面就详细介绍一下。关于OpenCV自适应直方图均衡CLAHE详细源代码请参考《》。
二、图像分块坐标以及图像分块大小与图像的宽和高不能整除的处理
2.1、图像分块坐标
进行对比度受限的自适应直方图均衡处理时,首先是需要将图像按参数tileGridSize切分为若干子块,这样图像就分成了tileGridSize.height行和tileGridSize.width列。
对这种分块,每个分块在坐标体系进行标记的话,横向坐标范围为[0,tilesX_-1],纵向坐标范围为[0,tilesY_]。这种标记分块的坐标,它与像素坐标存在映射关系,但是独立于像素坐标体系,老猿称这种分块的坐标为图像分块坐标。
2.2、不能整除的处理
当图像的宽(或高)不是对应横向(或纵向)分块数的整数倍时,老猿认为对于分块的处理有多种方式:
通过阅读源代码,OpenCV中采用将图像补齐到可以整除的大小,即对于图像的宽(或高)不是对应横向(或纵向)分块数的整数倍时,将对应宽(或高)补齐到可以整除的最少像素素。
具体处理的源代码如下:
if (_src.size().width % tilesX_ == 0 && _src.size().height % tilesY_ == 0)
{
tileSize = cv::Size(_src.size().width / tilesX_, _src.size().height / tilesY_);
_srcForLut = _src;
}
else
{
{
cv::copyMakeBorder(_src, srcExt_, 0, tilesY_ - (_src.size().height % tilesY_), 0,
tilesX_ - (_src.size().width % tilesX_), cv::BORDER_REFLECT_101);
tileSize = cv::Size(srcExt_.size().width / tilesX_, srcExt_.size().height / tilesY_);
_srcForLut = srcExt_;
}
}
上述代码中,src是输入图像矩阵,tilesX_是横向分块数,tilesY_是纵向分块数,因此图像被分成了tilesX_*tilesY_个分块。
三、CLIP的赋值和裁剪过程
3.1、CLIP的赋值过程
CLAHE涉及clipLimit的关键源代码摘要如下:
CLAHE_Impl::CLAHE_Impl(double clipLimit, int tilesX, int tilesY) :
clipLimit_(clipLimit), tilesX_(tilesX), tilesY_(tilesY)
{
}
void CLAHE_Impl::apply(cv::InputArray _src, cv::OutputArray _dst)
{
...
int histSize = _src.type() == CV_8UC1 ? 256 : 65536;
...
if (_src.size().width % tilesX_ == 0 && _src.size().height % tilesY_ == 0)
{
tileSize = cv::Size(_src.size().width / tilesX_, _src.size().height / tilesY_);
_srcForLut = _src;
}
...
const int tileSizeTotal = tileSize.area();
...
int clipLimit = 0;
if (clipLimit_ > 0.0)
{
clipLimit = static_cast(clipLimit_ * tileSizeTotal / histSize);
clipLimit = std::max(clipLimit, 1);
}
...
} 以上代码就是OpenCV自适应直方图均衡CLAHE对应源代码中关于clipLimit赋值处理的相关代码,可以看到,类设置方法中对clipLimit设置后,其值会保存在类私有变量clipLimit_ 中,最终进行apply自适应直方图均衡处理时,采用局部变量clipLimit = clipLimit_ * tileSizeTotal / histSize,并取clipLimit 和1中间的最大值。
可以看到,CLAHE中的clipLimit参数,最终被转换为了该值乘以tileSizeTotal (分块像素数)除以histSize(每个分块的直方图组数),这个转换是干什么呢?是得到每个分组的平均像素数量,如果灰度比较平均的话,每种级别(对应直方图分组数)的灰度所对应的像素数应该相等,当用该平均值乘以clipLimit,得到的是超过平均值clipLimit倍的像素数,这个值就是裁剪的限制值,对于超过这个值的分组就得裁剪。
3.2、直方图裁剪处理过程
裁剪处理在类 CLAHE_Impl的apply方法里调用CLAHE_CalcLut_Body类的函数对象来实现的,CLAHE_Impl是createCLAHE生成CLAHE实例时真正使用的类,而CLAHE_CalcLut_Body类是生成真正的直方图灰度映射和进行裁剪的类。涉及裁剪的代码在CLAHE_CalcLut_Body的operator函数中。相关的关键源代码如下:
template
void CLAHE_CalcLut_Body::operator ()(const cv::Range& range) const
{
...
// clip histogram
if (clipLimit_ > 0)
{
// how many pixels were clipped
int clipped = 0;
for (int i = 0; i < histSize; ++i)
{
if (tileHist[i] > clipLimit_)
{
clipped += tileHist[i] - clipLimit_;
tileHist[i] = clipLimit_;
}
}
// redistribute clipped pixels
int redistBatch = clipped / histSize;
int residual = clipped - redistBatch * histSize;
for (int i = 0; i < histSize; ++i)
tileHist[i] += redistBatch;
if (residual != 0)
{
int residualStep = MAX(histSize / residual, 1);
for (int i = 0; i < histSize && residual > 0; i += residualStep, residual--)
tileHist[i]++;
}
}
...
}
}
从上述代码可以看出,具体裁剪处理时,对于直方图分组像素数超过clipLimit_的,则将该分组中超过clipLimit_的像素数累加到clipped局部变量中,然后将该直方图分组像素数强制设置为clipLimit_。
上述过程对当前块的所有分组都处理完成后,将超出后累加的clipped变量值按分组数平均分配到各分组中,如果存在不够平均分配的部分,则等间距按顺序插入到分组中,直到所有超出部分都分配到了对应分组。如直方图分组是256个,累加的clipped值是1027个,则先每个分组值加4,然后将剩余3个分别累加到第0、85、 170三个位置的直方图分组中。
四、插值处理
插值处理是CLAHE算法中理解最困难的,占了本人研究该算法最多的时间,整体算法近4个月研究中,插值算法的理解用了110多天,也是本人直方图处理一直未能学习完成的根本原因。为了介绍清楚插值处理的算法,下面分成几部分来介绍。
为了说清楚问题,会用到一幅进行直方图均衡处理的经典图像,这幅图像的源图(在老猿的机器上文件名为f:\pic\valley.png)如下:

4.1、为什么需要插值?
下面这幅图是clipLimit设置为4、tileSize设置为4×4(横向和纵向都划分为4块,共计16块)进行自适应直方图均衡CLAHE处理时没有进行插值后的效果图(这是老猿修改算法代码模拟的,因此已经不能称为CLAHE):

可以清晰地看到在各个分块之间有明显的灰度突变,整体图像成了棋盘分块一样,这就是图像处理中的“棋盘效应”。为了解决棋盘效应,在CLAHE算法中,必须对图像进行插值处理,插值的目的是为了消除各分块之间的突变。下图就是真正的CLAHE处理(clipLimit设置为4、tileSize设置为4×4)后的效果图;

4.2、关于CLAHE使用的插值算法
CLAHE插值处理算法使用的是双线性插值,关于图像处理中的双线性插值网上有一堆的资料介绍,大家可自己查阅,老猿推荐大家阅读《》。在这些介绍的图像处理中的双线性插值,都是基于四个点的灰度值来计算这个四个点中间的某点的灰度值,但CLAHE算法中的双线性插值并不是这样的,这也是老猿理解该算法这么困难的原因。
4.3、CLAHE双线性插值算法详解
4.3.1、CLAHE插值算法概述以及插值关联分块
在CLAHE算法中进行插值处理是在累积直方图计算和对比度裁剪之后完成的,此时每个分块的灰度映射表已经求出,需要根据每个分块的灰度映射表生成输出图像每个像素的灰度值,生成时使用了双线性插值,也就是要找到与该像素对应的4个灰度值以及对应的比率来进行双线性插值。
在具体查找4个参考的灰度值以及对应的比例时,CLAHE是根据当前像素的横坐标m以及纵坐标n来确认与该像素相关的4个分块(这4个分块老猿称之为插值关联分块),然后根据(m,n)在源图像的灰度值分别求得在这4个分块中直方图均衡后的灰度映射置,再根据该像素横坐标m以及点的位置距分块的横向距离在横向进行两次x方向的线性插值,再将两次线性插值的结果根据纵坐标n及点的位置距分块的纵向距离在纵向进行一次线性插值。
4.3.2、像素4个插值关联分块的确定过程
从上面介绍可以知道,需要找到每个输入图像像素点的4个分块进行插值,确认这4个分块的过程如下:
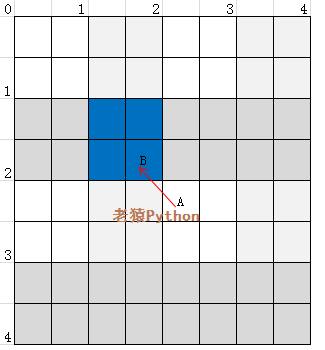
P右边分块PR对应坐标为(x+1,y)、其下边分块PD对应坐标(x,y+1)、其斜对角分块PRD对应坐标为(x+1,y+1),包括P在内这四个分块就是A的4个插值关联分块;
4个插值关联分块就是由2个横坐标值x和x+1以及2个纵坐标值y和y+1组合指定的分块;
四个插值关联分块中一定有一个为A所在分块、当B在图像范围内时一定也包含B所在分块,二者可能是同一分块,有可能是不同分块;
上图中这四个图像分块P(x,y)、PR(x+1,y)、PD(x,y+1)、PRD(x+1,y+1)的分块坐标分别为(1,1)、(1,2)、(2,1)、(2,2);
该虚拟扩展分块的分块坐标的x值或y值至少有一个小于0;
该虚拟扩展分块并没有真正的图像数据,没有对应的直方图均衡对应的灰度映射表,因此该虚拟扩展分块不能作为插值关联分块;
将该虚拟扩展分块小于0的坐标值强制设置为0,其他非0坐标值保持不变,得到的分块坐标对应分块就是插值关联分块。例如当x=-1时,关联的分块横坐标x和x+1值都是0,假设y大于等于0,则四个插值关联分块及其坐标为P(0,y)、PR(0,y)、PD(0,y+1)、PRD(0,y+1);
当B位于图像范围之外时,4个插值关联分块就会包含重复的分块,实际上可能4个分块对应的真正分块是2个分块(x、y中只有一个等于-1时)或者1个分块(当x=y=-1时);
这种情况意味着A所在范围为距图像边界在半个分块范围内,其目标图像的灰度值不用受其余分块的影响。
下图是一个分块为4×4时各个分块中的像素点对应的4个插值关联分块的横坐标和纵坐标取值:
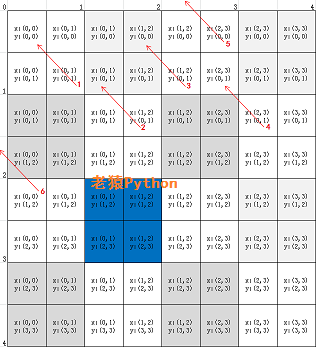
注意:
4.3.3、线性插值的比例确认
双线性插值实际上包含三次线性插值过程,前两次是x方向,最后一次是y方向,确认了4个插值关联分块之后,分别取原像素的灰度值在这4个分块的直方图均衡后灰度映射值(假设为r00、r01、r10、r11,其中r00表示映射点B所在分块的直方图均衡后的灰度映射值,r00、r01对应分块相邻在同一行,r10、r11对应分块相邻在另一行,而r00、r10对应分块相邻在同一列,r01、r11对应分块相邻在另一列),进行插值时,对于坐标为(m,n)的像素在x方向和y方向的插值比例是这样确认的:
下面是计算x方向插值比例的源代码:
float inv_tw = 1.0f / tileSize_.width;
for (int x = 0; x < src.cols; ++x)
{
float txf = x * inv_tw - 0.5f;
int tx1 = cvFloor(txf);
int tx2 = tx1 + 1;
xa_p[x] = txf - tx1;
xa1_p[x] = 1.0f - xa_p[x];
tx1 = std::max(tx1, 0);
tx2 = std::min(tx2, tilesX_ - 1);
}上面计算时,x为输入图像像素的横坐标,tileSize_是分块的大小,tileSize_的width为宽度、height为高度,inv_tw为分块宽度的倒数,xa_p[x]为映射点到其所在分块左边界的距离占分块宽度的比例,xa1_p[x]为到右边界的距离占分块宽度的比例,tx1和tx2为输入图像像素插值关联分块的2个分块横坐标。
下面是计算y方向插值比例的源代码:
float inv_th = 1.0f / tileSize_.height;
for (int y = range.start; y < range.end; ++y)
{
const uchar* srcRow = src_.ptr(y);//指向输入图像第y行数据
uchar* dstRow = dst_.ptr(y);//指向输出图像第y行数据
float tyf = y * inv_th - 0.5f;
int ty1 = cvFloor(tyf);
int ty2 = ty1 + 1;
// 差值作为插值的比例
float ya = tyf - ty1, ya1 = 1.0f - ya;
ty1 = std::max(ty1, 0);
ty2 = std::min(ty2, tilesY_ - 1);
} 上面计算时,y为输入图像像素的纵坐标,range.start=0,range.end等于图像的高度,inv_th为分块高度的倒数,ty1和ty2为输入图像像素插值关联分块的2个分块纵坐标。其中,ya和ya1是映射点到其所在分块上边界和下边界与分块高度的比例。
4.3.4、插值计算
假设输入图像中的像素A的映射点到B所在分块的分块坐标为(x,y),像素A的灰度值在4个插值关联分块的灰度映射值为r00、r01、r10、r11,其位置关系如前所述或编号对应坐标所示。对于B所在的分块,点B到分块(含虚拟扩展分块)四周的距离与分块宽或高的比例分别是x1、 x2、y1、y2,显然x1+x2=1、y1+y2=1。如图:
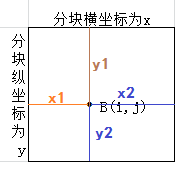
具体的插值计算过程如下:
ix1 = r00*x1+r01*x2
ix2 = r10*x1+r11*x2
dr = ix1*y1+ix2*y2
即:dr = ( r00*x1+r01*x2)*y1+( r10*x1+r11*x2)*y2 。
4.3.4、插值计算过程小结
对于4个插值关联分块是同一个分块时,r00=r01=r10=r11,x1+x2=1,y1+y2=1,dr的值就是在该分块内的灰度映射值;
当4个插值关联分块是分块纵坐标=0的分块时(即第一行分块),实际对应两个分块,r00=r10,r01=r11,此时:
dr =( r00*x1+r01*x2)*y1+( r00*x1+r01*x2)*y2
= r00*x1*(y1+y2)+ r01*x2*(y1+y2)
= r00*x1+ r01*x2
实际上就是一次x方向的插值;
4个插值关联分块是分块横坐标=0的分块时(即第一列分块),实际对应两个分块,r00=r01,r10=r11,x1+x2=1,此时:
dr =( r00*x1+r00*x2)*y1+( r10*x1+r10*x2)*y2
= r00*y1+r10*y2
实际上就是一次y方向的插值。
4.3.5、插值关联分块的获取方法背后的考量
在通过代码解读研究清楚了插值计算过程后,老猿反过头来理解这个计算过程的背后根由,其实这个背后根由很简单:
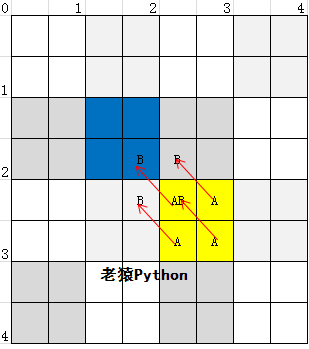
可以看到,这种移位后的映射点所在分块、左边分块、下边分块和右下对角分块这4个插值关联分块是与A所在位置最近的几个分块,并且包含了A所在分块自身;
最妙的是当B位于图像之外时,通过强制将小于0的分块坐标值设置为0后,插值关联分块中就存在重复分块,通过插值关联分块的双线性插值,对这些特殊情况就变成了非插值或者线性插值,有机的将所有情况的插值算法进行了统一,而不用区分所在位置。
五、小结
本文介绍了OpenCV对比度受限的自适应直方图均衡CLAHE算法,并通过代码研读详细剖了算法中的图像分块整除问题、直方图裁剪过程以及图像插值算法。相关内容在网上公开资料中没有公布,是老猿断断续续花费了4个月时间研究剖析,并在春节期间花了大量精力整理的,对计算机视觉算法感兴趣但不熟悉自适应直方图均衡CLAHE算法的各位同好应该是非常有帮助的资料。